What drives VXX price changes?

We have just finished the fourth day of our Quantitative Investing Festival 2021. We shared about volatility and how it has entered the mainstream via exchange-traded products that are traded like stocks. Volatility is quite a technical topic and it is difficult to go into certain specific details in a webinar. So in this blog post, we will look specifically at how the price of a very popular exchange-traded product called VXX is derived.

What is VXX?

First, let's briefly look at what is VXX. You can read the product summary from the issuer website but in essence, VXX tracks the daily returns of the S&P 500 VIX Short-Term Futures Index Total Return. This Index replicates a rolling exposure to a constant 30-day VIX futures contract and it is a synthetic combination of the first and second-month VIX futures contracts which gives a weighted time to expiry of 30 days. Do not worry if you still do not follow because the illustrated example below should make it clear.

VIX Term Structure

Let's use an imaginary VIX term structure to illustrate how the constant 30-day VIX futures contract is derived.

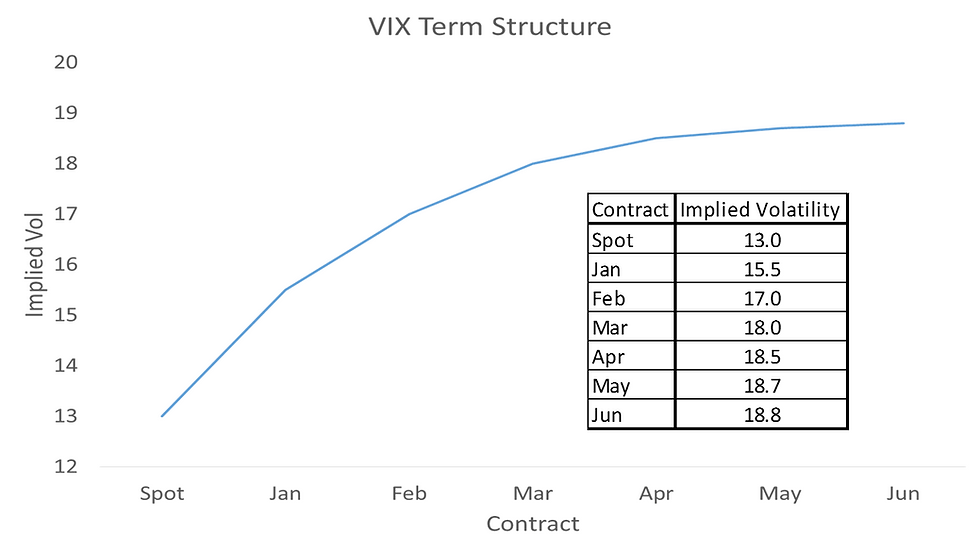
The term structure is a plot that shows the prices of the various VIX futures contracts with different maturity dates including the spot VIX which is the current VIX price. The x-axis shows the maturity dates of the contracts in ascending order starting with Spot VIX then followed by the contract that is first to expire and so on. The y-axis shows the implied volatility of the respective contracts. This implied volatility is also the price of the futures contract since they are quoted in volatility terms. Let's assume that all the futures prices do not change and remain fixed at current levels. Let's further assume that the Jan contract has 15 days to expiry and the Feb contract has 45 days to expiry. So let's determine what mix of the Jan and Feb contracts would give a synthetic 30-day contract.

Constant 30-Day VIX Futures Contract

This first example is the simplest as the 30-day is right smack in the middle of the Jan and Feb contracts so we simply need to have equal amounts of both contracts to give a weighted 30-day maturity. Therefore the synthetic price of this 30-day contract can be calculated using the formula below. Since there are 30 days to expiry, it is easier to calculate in parts of 30. So we need 15 Jan contracts and 15 Feb contracts.

After 5 days have passed, the Jan contract is now left with 10 days to expiry and the Feb contract with 40 days to expiry. The Jan contract is now further away from the 30-day contract while the Feb contract is moving closer. Hence, we need less of Jan and more of Feb. To be exact, we need 10 Jan contracts and 20 Feb contracts. So we need to sell 5 Jan and buy 5 Feb. We use 5 days interval here but the issuer does this daily.

After another 5 days, the Jan contract is now only 5 days to expiry and the Feb contract is 35 days away. So we need to sell another 5 Jan and buy 5 more Feb.

After yet another 5 days, the Jan contract expires and the Feb contract is now the exact 30-day contract so the price of the 30-day is the same as the Feb contract which is 17. The Jan contract is now out of the picture and the Mar contract comes in.

So after another 5 days, the Feb contract is 25 days to expiry and the Mar contract is 55 days to expiry. We need to sell 5 Feb contracts and buy 5 Mar contracts.

Rolling Cost

In the exercise above, it seems like the 30-day futures price keeps going up as time passes so some clarification is needed. For the exercise, we assumed that all the futures prices remain unchanged even as they approached expiry. In reality, the futures prices converge to spot VIX as they approach expiry. Hence, the Feb contract converges to the Jan contract while the Jan contract converges to spot. Hence, if the term structure remains unchanged, the synthetic 30-day futures price should also remain unchanged. Now, if the S&P 500 VIX Short-Term Futures Index Total Return is supposed to track the 30-day futures price, then theoretically the Index price should also remain unchanged. However, as we have seen in the exercise above, we need to constantly sell the expiring futures at a lower price and buy the next futures at a higher price to maintain the constant 30-day maturity. This incurs a real cost that is factored into the Total Return Index.

Hence, even if the 30-day futures price doesn't change, the Index will slowly lose its value over time. This is the rolling cost incurred whenever the term structure is in contango which is when the nearer futures are cheaper than longer-dated futures. When the term structure is inverted (the technical term is backwardation) which is when the nearer futures are more expensive than longer-dated futures, the opposite is true. The Index gains from rolling as the issuer is selling the expiring futures at a higher price and buying the next futures at a lower price.

Conclusion

Through tracking the daily returns of the S&P 500 VIX Short-Term Futures Index Total Return, there are two main drivers for VXX price changes.

1. The price change in the synthetic constant 30-day VIX futures contract.

2. The rolling cost associated with maintaining this constant 30-day exposure.

I hope you have a better appreciation of how the VXX works and how you can tie its movements to the VIX Index which is popularly known as the fear gauge.